
Sum by Factors, CodeWars Kata
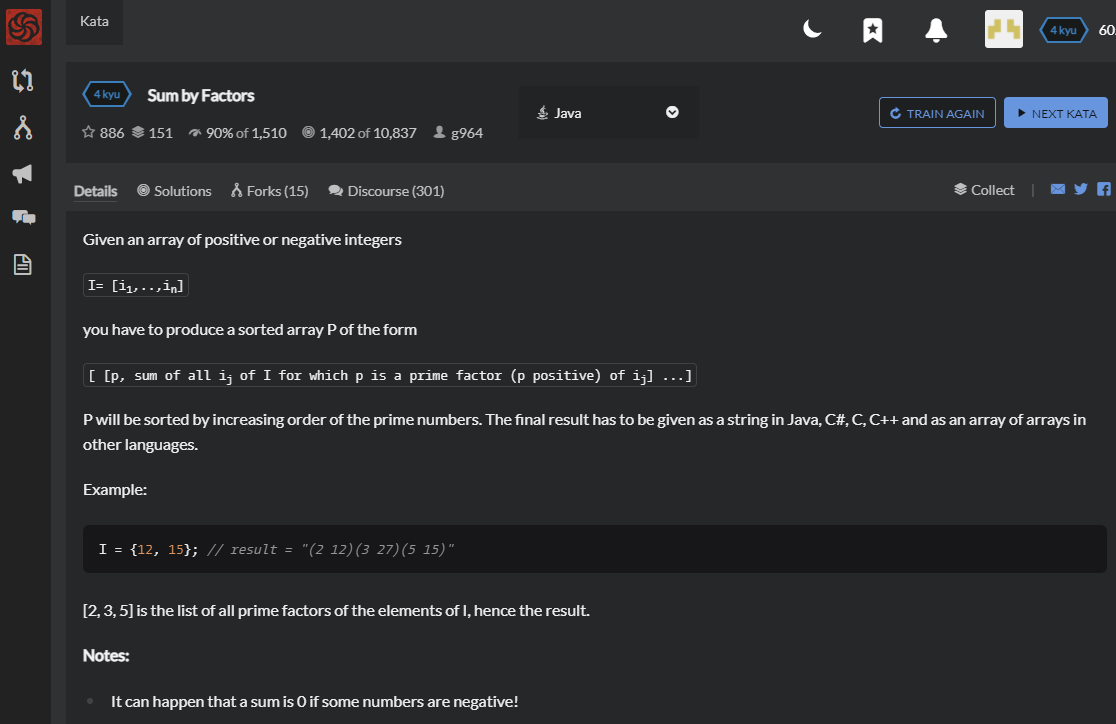
Given an array of positive or negative integers
I= [i1,..,in]
you have to produce a sorted array P of the form
[ [p, sum of all ij of I for which p is a prime factor (p positive) of ij] ...]
P will be sorted by increasing order of the prime numbers. The final result has to be given as a string in Java, C#, C, C++ and as an array of arrays in other languages.
Example:
I = {12, 15}; // result = "(2 12)(3 27)(5 15)"
[2, 3, 5] is the list of all prime factors of the elements of I, hence the result.
Notes:
- It can happen that a sum is 0 if some numbers are negative!
Example: I = [15, 30, -45] 5 divides 15, 30 and (-45) so 5 appears in the result, the sum of the numbers for which 5 is a factor is 0 so we have [5, 0] in the result amongst others.
- In Fortran - as in any other language - the returned string is not permitted to contain any redundant trailing whitespace: you can use dynamically allocated character strings.
문제 해석
문제를 이해하기가 제일 어려웠던 문제입니다. 주어진 입력 문자열 중 소수를 약수로 가지는 수들만 더해서 합을 같이 출력합니다. 예문을 살펴보면, 12는 소수 중 2와 3을 약수로 가집니다. 15는 소수 3을 약수로 가지죠. 그래서 출력 배열에서 2는 2를 약수로 가지는 12와 짝이 되고요. 3은 3을 약수로 가지는 12, 15 의 합과 짝이 되어 27과 짝이 됩니다.
입력값
- int[] l: 입력 배, I의 원소는 음수일 수도 있습니다.
출력값
- String: 약수인 소수와 그 소수가 약수인 숫자들의 합 배열을 문자열로 표현. (소수, 소수가 약수인 숫자들의 합)...
My Solution
먼저 소수인지 아닌지를 판별하는 isPrime(int num)을 정의했습니다. 이 메소드에서는 주어진 숫자의 1/2+ 1까지 탐색하면서 나누어 떨어지는 값이 있는지 확인합니다. 나누어 떨어지는 값이 없다면 1과 자신만을 약수로 가지는 소수입니다.
솔루션 메소드 String sumOfDivided(int[] l)에서는 주어진 문자열 중 최고 값을 찾아 2부터 최고 값까지 루프를 돌렸습니다. 먼저 2부터 증가하는 이 값이 소수인지 판별하고요. 소수라면 입력배열 I중에서 이 소수를 약수로 가지는 원소들을 찾아서 합을 구하고 출력값들을 저장하는 ArrayList<String> list에 넣었습니다.
import java.util.ArrayList;
import java.util.Arrays;
import java.util.stream.Collectors;
public class SumOfDivided {
public static String sumOfDivided(int[] l) {
ArrayList<String> list = new ArrayList<String>();
System.out.println(Arrays.stream(l).map(item -> Math.abs(item)).max().getAsInt() + 1);
for (int i = 2; i < Arrays.stream(l).map(item -> Math.abs(item)).max().getAsInt() + 1; i++) {
for (int num : l) {
if (num % i == 0 && isPrime(i)) {
final int prime = i;
list.add(String.format("(%d %d)", i, Arrays.stream(l).filter(item -> item % prime == 0).sum()));
break;
}
}
}
return list.stream().collect(Collectors.joining(""));
}
public static boolean isPrime(int num) {
for (int i = 2; i < num / 2 + 1; i++) {
if (num % i == 0) {
return false;
}
}
return true;
}
}
Best Practice
BP에서는 저와 마찬가지로 입력배열의 절대값 중 가장 큰 값을 이용했습니다. 저와는 다르게 최대 값 이내의 소수를 먼저 구하는 메소드List<Integer> eratosteneSieve(final int x)를 작성했네요.
이렇게 소수의 리스트를 먼저 구한 다음 이 리스트를 Stream으로 처리하면서 입력배열 중 소수를 약수로 가지는 값들을 reduce를 통해 처리했네요. Stream을 적극적으로 사용하고, Stream.reduce() API를 적절하게 잘 사용한 BP입니다.
import java.util.Arrays;
import java.util.List;
import java.util.stream.Collectors;
import java.util.stream.IntStream;
public class SumOfDivided {
public static String sumOfDivided(int[] l) {
final int maxValue = Arrays.stream(l).map(num -> Math.abs(num)).max().getAsInt();
return eratosteneSieve(maxValue).stream()
.reduce("",
(resultString, primeNum) -> {
List<Integer> divisibleNum = Arrays.stream(l).filter(num -> num % primeNum == 0).boxed().collect(Collectors.toList());
return divisibleNum.size() > 0
? resultString + String.format("(%d %d)", primeNum, divisibleNum.stream().mapToInt(Integer::intValue).sum())
: resultString;
},
(not, used) -> null);
}
public static List<Integer> eratosteneSieve(final int x) {
final List<Integer> candidates = IntStream.rangeClosed(2, x).boxed().collect(Collectors.toList());
return candidates.stream()
.filter(num -> num <= Math.sqrt(x))
.reduce(candidates,
(resList, currNum) -> resList.stream()
.filter(num -> num % currNum != 0 || num.equals(currNum))
.collect(Collectors.toList()),
(not, used) -> null);
}
}
'IT Contents > 프로그래밍 팁' 카테고리의 다른 글
| Befunge Interpreter, CodeWars Kata 자바 솔루션 (0) | 2021.04.19 |
|---|---|
| Codewars style ranking system, CodeWars Kata 자바 솔루션 (0) | 2021.04.18 |
| Strip Comments, CodeWars Kata 자바 솔루션 (0) | 2021.04.16 |
| Integers: Recreation One, CodeWars Kata 자바 솔루션 (0) | 2021.04.15 |
| What's a Perfect Power anyway?, CodeWars Kata 자바 솔루션 (0) | 2021.04.14 |





최근댓글